通常の気体熱伝導率との違い「エネルギー理工学設計演習・実験２」別冊
1998.08.29 I.Takagi
keywords: thermal conductivity of free molecules
概要
圧力が低い（平均自由行程λが代表長さｄよりも充分大きい）場合の、気体の熱伝導率を導き、熱流束が圧力に比例することを示します。
通常の気体熱伝導率との違い
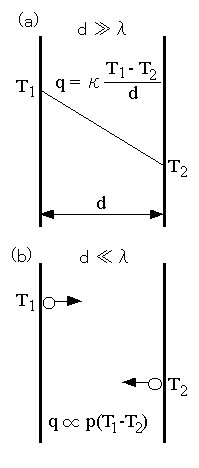
右図(a)に示すように、気体を挟んで平行に置かれた無限平板があり、それぞれ、温度が Ｔ1 と Ｔ2 （Ｔ1>Ｔ2）に保たれているものとします。板の間隔 ｄ が平均自由行程λ よりも充分大きい場合（λ≪ｄ）、定常状態における熱流束 ｑ は、
ｑ = κ(Ｔ1−Ｔ2)/ｄ (1)
と表されます。ここに、κは気体の熱伝導率です。板に挟まれた部分の気体の温度は図示するように、直線的に変化します（注１）。このような条件での熱の輸送をミクロに眺めてみると、次のようになります。
簡単のため、板に垂直な方向のみの分子の運動を考えます。板１に衝突した分子は、 Ｔ1 の温度になって跳ね返ります（注２）。この分子はλ程度進んだ位置で他の分子と衝突して熱の一部を伝え、温度が少し下がります。衝突された分子は、λ程度進んだ位置で他の分子と衝突し、板２に至るまで次々と熱が伝わって行きます。板の間隔 ｄ はλよりも非常に大きいので、板１から２に熱が伝わるまでには、無数の衝突が介在します。その結果、気体の温度は Ｔ1 から Ｔ2 まで滑らかに変化（図の例では直線的に減少）します。（１）式右辺の ｄ は、板１から板２に熱が輸送されるまでに起こる分子の衝突数とも考えられ、この数が多いほど（ｄが大きいほど）熱が伝わりにくい、つまり熱流束 ｑ が小さくなります（注３）。
次に、ｂ図に示すように、熱が次々と伝わらずに板１から２に一気に伝わる場合、つまり ｄ≪λ の場合を考えてみます。ある分子に注目すると、板１に衝突して温度 Ｔ1 で跳ね返った分子は、途中で他の分子と衝突することなく、板２に衝突し、温度 Ｔ2で跳ね返って再び板１に衝突するという単純な往復運動を繰り返すでしょう。ｄ≪λの条件が満たされる限り、板の間隔が広くなっても狭くなっても、単位時間・単位面積当たりに板１や板２に衝突する分子の数は変わりませんから、輸送される熱量 ｑ も変わらない筈です。従って、このような条件（分子流の条件）下では、ｑ は ｄ に依存しません。一方、ｑ は分子の衝突頻度に比例しますから、圧力 ｐ に比例すると予想されます。そこで、比例定数を Λとすると、
ｑ = Λｐ（Ｔ1−Ｔ2） (2)
と表されます。このΛは、自由分子の熱伝導率と呼ばれています。（２）式の形を見ると、Λｐが熱伝達係数と同じ次元を持つことがわかります。
代表長さとは？
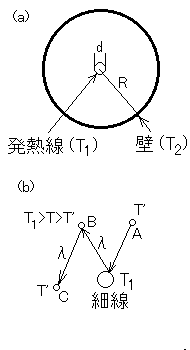自由分子熱伝導率を導く前に、代表長さについて検討しておきます。上記の例では、平均自由行程と比較される対象（代表長さ）は、板の間隔
ｄ ですが、ピラニ真空計（右図(a)）のように、発熱する細線を温度の低い壁が囲んでいる場合はどの長さを対象とすればよいでしょうか？答えは壁の内半径
Ｒ ではなく、細線の直径 ｄ になります。
右図(b)で、Ａの位置から細線に衝突した分子が、温度Ｔ1となって跳ね返るものとします。また、周囲の気体の温度を Ｔ' とします。この分子はλ程度進んだＢの位置で他の分子と衝突し、Ｔ1より少し低い温度 Ｔ （ Ｔ' よりも高い温度）になります。もし、この分子がＢの位置から再び細線に衝突する確率が高ければ、つまり、細線の直径 ｄ がλより充分大きければ、Ｔ' よりも高い温度 Ｔ の分子が数多く細線に衝突することになり、細線と周囲の気体との間には温度勾配が生じてしまいます。しかし、ｄ≪λであれば、Ｂの位置から細線に向かう分子はほとんど無く、例えばＣの位置で次の衝突を起こします。このようにして、一旦細線で跳ね返った分子は、次に細線に衝突する前に、周囲の温度と平衡になると考えられます。しかも ｄ が小さいので、細線に衝突する分子の数は少ないのに対し、壁に衝突する分子の数は非常に多いため、Ｔ' は壁の温度Ｔ2 とほとんど同じになります。
以上の説明から、図(a)のような場合には、線の直径 ｄ が代表長さであることがわかると思います。実際に、ｄ = 25μm、Ｒ = 8mm のピラニー真空計の特性によると、空気の圧力が 30Pa (λ〜250μm) 以下で（２）式が成り立つことが示されている。もし、代表長さを Ｒ と考えると、λ = 90mm となる圧力は 0.1Pa 以下となってしまい、30Pa まで（２）式が成り立つことを説明することはできません。
本題に入る前に説明が長すぎたかもしれませんが、真空工学や気体分子運動論の教科書では、代表長さをどのようにとるべきか解説していることが少ないため、ここでやや詳しく述べておきました。
自由分子熱伝導率Λ
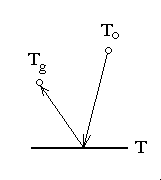
右図に示すように、一定の温度 Ｔ に保たれた面があり、周囲の気体は温度 Ｔo と平衡になっているものとします。これは、上に述べた細線の例の場合に相当しており、細線表面を拡大して示していると考えればよいでしょう。ただし、より現実的に取り扱うため、面で跳ね返った分子の温度は Ｔg に相当するものとします。
単純に考えれば、分子当たりの比熱を ｃ' としますと、面に入射した分子が持ち込む熱量は ｃ'Ｔo、持ち去る熱量は ｃ'Ｔg であり、単位面積・単位時間当たりに面に入射する分子の数と跳ね返る分子の数は共に等しく、入射頻度ｎｖ/4 ですから、熱流束 ｑ は、
ｑ = ｎｖｃ'（Ｔg−Ｔo）/4 (3)
と表されます。ここに、ｎ と ｖ はそれぞれ、周囲の気体分子の密度と平均速さです。次に、
α = （Ｔg−Ｔo）/（Ｔ−Ｔo） (4)
というパラメータを導入し、理想気体を仮定（ ｐ = ｎｋＴo ）しますと、（３）式は、
ｑ = α（ｃ'ｖ/4ｋＴo）ｐ（Ｔ−Ｔo） (5)
と書き換えられます。α は適応係数 (accommodation factor) と呼ばれ、分子と固体との熱の授受における効率を表します。（４）式からわかるように、分子が温度 Ｔ で跳ね返ったとしますと、α = １ です。 （２）式ではα = 1 と考えていることに注意すると、自由分子熱伝導率Λとして、ｃ'ｖ/4ｋＴo が得られます。
（３）式中の ｃ' は定積比熱では無いことに注意する必要があります。単原子分子では、分子の熱エネルギーは並進の運動エネルギーですから、分子が持ち込む熱量 ｃ'Ｔ は ｍｖ2/2 であり、２乗平均速さの関数です。つまり、（３）式では分子の速さに分布があることを無視し、ｖ と ｖ2 を単純に乗じていることになります。従って、ｃ'Ｔ は以下の式で表されるように、ｖｆ(ｖ) を重みとした ｍｖ2/2 の平均値として表されなければなりません。
ｃ'Ｔ = ∫(ｍｖ2/2)ｖｆ(ｖ)ｄｖ/∫ｖｆ(ｖ)ｄｖ (6)
ここに、ｆ(ｖ)ｄｖ は速さの分布関数であり、 Ｃ を定数とすると Ｃｖ2exp(−ｍｖ2/2ｋＴ)dｖ と表されます。積分範囲は分母、分子とも 0 〜 ∞ です。平均速さ ｖ が ∫ｖｆ(ｖ)ｄｖ であることを考慮すると（６）式の分母は簡単に積分でき、ｃ'Ｔ = 2ｋＴ が得られます。定積比熱を ｃ とすると、単原子分子では ｃ = 3ｋ/2 ですから、
ｃ' = ｃ + ｋ/2 (7)
となります。
（７）式は、並進の運動エネルギーの比熱への寄与は、固体への衝突現象を対象とする場合には、2ｋ であることを示しています。多原子分子の場合、並進運動の他に回転や振動が加わりますが、回転と振動のエネルギーは、分子の並進エネルギー、つまり速さに無関係ですから、（７）式は他原子分子に対しても適用することができます。但し、この場合の ｃ の値は、２原子分子では 5ｋ/2 になります。（７）式を一般的に表すために、ｃp−ｃ = ｋ （ｃpは定圧比熱）と γ = ｃp/ｃ の関係式を導入すると、
ｃ' = ｋ(γ+1)/2(γ-1) (8)
を得ます。γは比熱比と呼ばれており、単原子分子では 5/3、２原子分子では 7/5 です。
（８）式と（５）式より、熱流束 ｑ と自由分子熱伝導率Λは、それぞれ、
ｑ = αΛｐ（Ｔ−Ｔo） (9)
Λ = (γ+1)/2(γ-1)×(ｋ/2πｍＴ') 1/2 (10)
と表されます。ただし、Ｔ' = (Ｔ+To)/2 です（注４）。例えば、面の発熱量ｑ と周囲の温度 Ｔo が既知で Ｔ が未知のような場合は、最初は Ｔ' = To とおいて Ｔ を求め、次に Ｔ' = (Ｔ+To)/2 として Ｔ を求め直すといった繰り返し計算をしますが、Ｔ がそれほど To と違わない場合には、単純に Ｔ' = Ｔo としても構わないでしょう。
具体的な数値
温度 Ｔ' が 273K である窒素ガスについて自由分子熱伝導率Λ を（１０）式から求めると、γ = 1.4 より、1.2 m/sK を得ます。ちょっと奇妙な単位ですが、ｐ を Pa (N/m2) で、ｑ を W/m2で表し、（９）式に代入すると確かにこのようになります。
(注1)κは温度に依存するから、厳密に言えば正しくない。ここでは、話を簡単にするためにκは温度に依存しないものと考える。 (注２)実際にはＴ1よりも低い場合が多く、これについては後述する。 (注３)圧力が高くなるとλが小さくなり、ｄが一定でも衝突する数は増える。しかし、この場合には熱の担い手である分子の数が増えるので、両者は相殺してしまう。本文の説明は、ｄが単純に大きくなった場合についてのものであることに注意せよ。 (注４) Ｔ' の厳密な取扱はやや複雑であり、ここでは直感的な算術平均を用いることにした。
以上
このページは、高木郁二が担当している京都大学工学部物理工学科の講義・実験を補う資料として作成したものです。ご意見・お問い合わせはこちらまでお願いします。