 熱伝導率とは?
熱伝導率とは?「エネルギー理工学設計演習・実験2」別冊
1998.08.22 I.Takagi 2000.11.09 Rev.1
keywords: thermal conductivity of gas
概要
圧力が高い(平均自由行程λが代表長さ L よりも充分小さい)場合の、気体の熱伝導率を導き、その値が圧力に無関係であることを示します。逆の場合(λ≫ L )については次のページで説明します。
 熱伝導率とは?
熱伝導率とは?
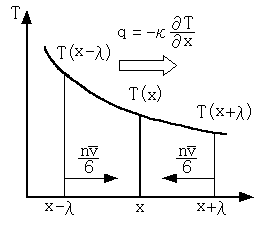
温度が一様で無い物質(固体でも液体でも気体でもよい)を考えます。例えば、右図に示すように、x方向に温度勾配が存在し、温度 T が x の関数 T(x) であるとします。熱は温度の高い方から低い方へ移動しますので、位置 x において、単位面積・単位時間当たりに横切る正味の熱の流れ(熱流束) q は、0ではありません。この q が温度勾配 -∂T/∂x に比例する(注1)と考えたときの比例定数 κ を熱伝導率といいます。つまり、
q = -κ(∂T/∂x) (1)
と表されます。
簡単な導き方
物質が気体の場合、熱は気体分子の運動によって運ばれます(注2)。分子は他の分子と衝突する度に運動エネルギーの一部を渡したり、貰ったりするためです。衝突した分子が、次に運動エネルギー(熱)の授受をするまでに移動する距離は平均自由行程λですから、図に示すように、微小な距離(注3)をλとし、位置 x-λから正の方向に移動した温度 T(x-λ) の分子は、位置 x で衝突して温度 T(x) となると考えます。分子当たりの定積比熱を c としますと、正の方向に輸送された正味の熱量は、1分子当たり c[T(x-λ)-T(x)] となります。同様に、位置 x+λから負の方向に移動した分子は位置 x で衝突し、c[T(x+λ)-T(x)] の熱量をもたらすと考えます。
分子の入射頻度は、単純な仮定(全分子の1/6が正の x 方向に進む)によると nv/6 です。ここに、n と v はそれぞれ、分子の密度と平均速さです(注4)。従って、単位面積・単位時間当たり輸送される熱量(熱流束) q は、流れの向きを考慮すると、
q = (nv/6)c[T(x-λ)-T(x)] -(nv/6)c[T(x+λ)-T(x)] (2)
と表されます。λは微小な区間であることより、T(x-λ) を1次の項まで展開すると、
T(x-λ) = T(x)-λ(∂T/∂x) (3)
ですから、(3)式は
q = -(nvcλ/3)(∂T/∂x) (4)
となります。(4)式と熱伝導率を定義した(1)式を比較することにより、熱伝導率κは、
κ = nvcλ/3 (5)
と表されることがわかります。
 熱伝導率κの性質
熱伝導率κの性質
分子の衝突に関する全散乱断面積をσとしますと、平均自由行程λは 1/21/2nσ (A-3 (6)式参照)と表されますので、(5)式は、
κ = cv/(3・21/2σ) (6)
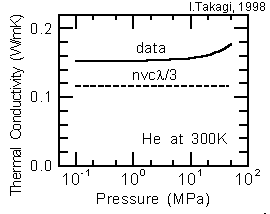
となり、熱伝導率は圧力に依存しないという結果が得られます。圧力が減少すると、衝突する頻度(熱の授受を行う機会)も減少しますが、次の衝突までの距離(熱を伝える長さ)は増加し、これらの効果が相殺するためです。実際、ヘリウムの熱伝導率(注5)は、右図に実線で示すように、0.1 MPa (大気圧) から 10 MPa(100気圧) までは圧力にほとんど依存していません。図中の破線は、(6)式によって求めた値ですが、単純な仮定(後述します)に基づいて導いた割には、良く一致しています。なお、(6)式中では、c = 3k/2 、σ = πd2/4 ( d = 0.258nm (注6)) としました。
次に温度への依存性を考えてみます。分子当たりの定積比熱 c は単原子分子では 3k/2、2原子分子では 5k/2 等と表されますので、温度には依存しません。また、全散乱断面積は、分子が剛体球であると仮定しますと、上にも記したように、分子直径 d の2乗に比例するだけですので、これも温度に無関係です。一方、平均速さ v は、絶対温度 T の平方根に比例します。以上から、熱伝導率κは温度の平方根に比例することになり、(6)式は
κ = (4k/πd2)(kT/πm)1/2 (7)
と書くことができます。ここに、mは分子の質量です。
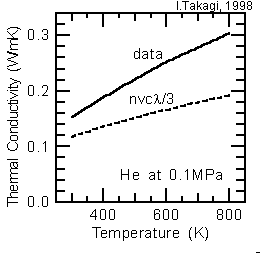 上の例と同様に、ヘリウムについて実際の値(注7)と(7)式による計算値とを比較しますと、右図のようになります。絶対値はともかく、実際の値の温度依存性は、T0.5ではなく、T0.6程度になっていますが、これは、剛体球と仮定して分子直径
dを定数としたためと考えられます。Lennard-Jones
のポテンシャルを仮定すれば、温度が高いと分子どうしはより近くまで接近することができ、分子直径 d は小さくなることになりますので、定性的には実際の値の傾向を説明することができます。
上の例と同様に、ヘリウムについて実際の値(注7)と(7)式による計算値とを比較しますと、右図のようになります。絶対値はともかく、実際の値の温度依存性は、T0.5ではなく、T0.6程度になっていますが、これは、剛体球と仮定して分子直径
dを定数としたためと考えられます。Lennard-Jones
のポテンシャルを仮定すれば、温度が高いと分子どうしはより近くまで接近することができ、分子直径 d は小さくなることになりますので、定性的には実際の値の傾向を説明することができます。
仮定した条件について
上の2つの図で示したように、(5)式あるいは(7)式から求めたκの値は、実際の値とは若干異なります。そこで、これらの式を導く際に(暗黙の内に)仮定した条件について検討しておきます。
先ず、任意の位置を横切る流れは nv/6 であると考えましたが、これは2つの点で正確ではありません。1つは、分子の入射頻度は nv/4 であることです。しかし、nv/4 を用いて計算する場合、微小な区間としてλの x 方向の平均値 (2λ/3 になる) を取らなければならなりませんから、結局、(5)式の形は変わりません。もう1つは、温度勾配が存在するために、位置によって nv の値が異なることです。圧力 p は位置によらず一定ですから、理想気体の関係 p = nkT と、kTが v2 に比例することから、nv2 が位置によらず一定であり、nv は一定では無いことがわかります。また、温度勾配が存在する場合には、速さの分布は Maxwell 分布から若干ずれてしまいますので、v = (8kT/πm)1/2 にはならないことも挙げられます。このほか、(5)式を導く際、例えば位置 x -λから移動して位置 x で衝突した分子の温度は T(x) になると仮定しました。しかし、実際には 1回の衝突で周囲の温度である T(x) になるとは限りません。
全散乱断面積σを定数と仮定しましたが、上で述べたように分子直径 d は温度の増加と共に減少するため、σ も減少します。この影響はκの温度依存性に現れています。
(注1) 温度が高い方から低い方への熱の流れを正にとるため、負号が付く。 (注2) 輸送現象と言う。 (注3) 図からは微小な距離に見えないかもしれないが、熱の移動が起こっている長さL(例えば容器の壁間)はλよりもずっと大きい場合を考るものとする。 (注4) 平均値は図に示すように文字の上に横棒を引いて表現するのが一般的であるが、HTMLにはその機能が無いため、下線で示した。 (注5) 日本機械学会編「伝熱工学資料(第4版)」丸善(1986)337. (注6) B.H.Mahan著、塩見賢吾ら訳「大学の化学[Ⅰ]」廣川書店(1972)87. (注7) 熱量は温度 T(x) を基準にしているため、位置xにいた分子の移動は考慮しなくてよい。仮に他の温度を基準にしても、位置xからは正負の方向に同じ数の分子が移動するので、考慮しなくてよい。 (注8) 熱物性値のデータ集に記載された値であり、「実際」の値であるとは言えないかもしれないが、このように表現した。
Rev.1 の修正個所: √ がかかる範囲が不明瞭なので、表記を 1/2 に改めた。
以上
このページは、高木郁二が担当している京都大学工学部物理工学科の講義・実験を補う資料として作成したものです。ご意見・お問い合わせはこちらまでお願いします。