 速さ vで運動している気体分子は、他の気体分子に次々と衝突します(注2)。ある衝突から次の衝突までの時間の平均値を、平均自由時間τと呼ぶことにします。また、ある衝突から次の衝突までの飛行距離の平均値を、平均自由行程λと定義します。すると、
速さ vで運動している気体分子は、他の気体分子に次々と衝突します(注2)。ある衝突から次の衝突までの時間の平均値を、平均自由時間τと呼ぶことにします。また、ある衝突から次の衝突までの飛行距離の平均値を、平均自由行程λと定義します。すると、「エネルギー理工学設計演習・実験2」別冊
1998.08.01 I.Takagi 1998.08.13 Rev.1 2000.11.09 Rev.2
keywords: mean free path of gas molecules
概要
気体分子の平均自由行程λは、気体中の輸送現象(熱や物質の移動)を理解する上で重要なパラメータで、真空工学でも頻繁に登場します。先ずは単純な仮定を用いてλがどのような式で表されるかを導き、続いてより現実に近い条件下での式を導きます。
前提として、
・気体は熱的に平衡であり、 ・気体は充分希薄である
ものとします。後者はいくつかの意味を持っており、例えば、理想気体の状態方程式が成り立つとか、3重衝突と見なされるような衝突は起きないとか、あるいは、Dulong-Petitの法則(補足) で述べたように、量子力学的な効果は無視できるとかです。
最も単純に考えた場合
以下の仮定または条件を設けます。
・気体は1種類の分子から成っている。 ・気体分子は半径rの剛体球である。 ・ある分子1個のみが一定の速さvで運動し、他の分子は静止している。
最初の項目は条件ですが、2項目は仮定であり、例えば2原子分子が球体であるとは想像し難いですし、電子を纏っている原子が堅い殻であるはずがありませんが(注1)、よい近似で成り立っていると考えることにします。最後の仮定は導出を簡単にするために設けたものです。少々乱暴に思うかもしれませんが、全ての分子が運動している場合についてはこの次で説明します。
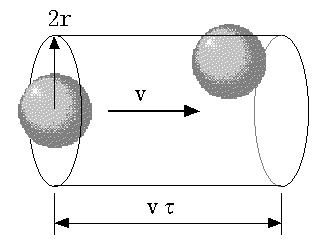
 速さ vで運動している気体分子は、他の気体分子に次々と衝突します(注2)。ある衝突から次の衝突までの時間の平均値を、平均自由時間τと呼ぶことにします。また、ある衝突から次の衝突までの飛行距離の平均値を、平均自由行程λと定義します。すると、
速さ vで運動している気体分子は、他の気体分子に次々と衝突します(注2)。ある衝突から次の衝突までの時間の平均値を、平均自由時間τと呼ぶことにします。また、ある衝突から次の衝突までの飛行距離の平均値を、平均自由行程λと定義します。すると、
λ = vτ (1)
という簡単な関係式が得られます。
右の図に示すように、速さ v で運動している分子が他の静止している(とここでは考えている)分子と衝突するのは、球の中心から 2r の範囲内にいる場合に限られます。つまり、運動している分子は半径 2r の大きさを持ち、他の分子は点と考えてもよいことになります。そこで、運動している分子の幾何学的な断面積 σ は、
σ = 4πr2 (2)
と表されます。分子の衝突は、その運動方向を変えることから散乱とも言えますので、σ を全散乱断面積と呼びます(注3)。「全」は、散乱後の方向を問わない(全ての散乱方向の総和を表す)ことを意味しています。運動している分子は、断面積 σ を持って λ(=vτ) だけ進む間に、平均して他の分子1個と衝突することになりますから、σvτは1つの分子が空間に占める体積の平均値を表します。従って、分子の密度を n とすると、
n= 1/(σvτ) (3)
と表されますので、(1)式より、
λ = 1/(nσ) (4)
が得られます。これが、最も単純に考えた場合の平均自由行程を表す式です。実際には他の分子も運動していますから、次に示す(5)式の方が正確ですが、平均自由行程は分子密度と散乱断面積に逆比例するということが(4)式からわかります。
全ての分子が運動している場合
もう少し現実的に取り扱うために、全ての分子が速度 v で運動していると考えると、条件は以下のようになります。
・気体は1種類の分子から成っている。 ・気体分子は半径rの剛体球である。 ・気体分子は一定の速さvで運動している。
この場合でも(1)式は成り立ちますが、(3)式中の v は、分子どうしの相対的な速さの平均値 u に置き換えなければなりません。
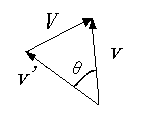 2つの分子の相対速度をV (ベクトルを斜体で表します)
とすると、2つの分子の速度 v と v' との間には右図のような関係があり、余弦定理より、V2
= v2 + v'2 -2vv'cosθ です。ここで、両辺の平均を取ると左辺は
u2 です。また、v と v' のなす角 θは全くランダムですから、cosθの平均値は
0 となります。条件より分子の速さ v は一定ですから、右辺第1項と第2項は共にv2 です。従って、与式は
u2 = 2v2 となりますので、(3)式は
2つの分子の相対速度をV (ベクトルを斜体で表します)
とすると、2つの分子の速度 v と v' との間には右図のような関係があり、余弦定理より、V2
= v2 + v'2 -2vv'cosθ です。ここで、両辺の平均を取ると左辺は
u2 です。また、v と v' のなす角 θは全くランダムですから、cosθの平均値は
0 となります。条件より分子の速さ v は一定ですから、右辺第1項と第2項は共にv2 です。従って、与式は
u2 = 2v2 となりますので、(3)式は
n = 1/(21/2vστ) (5)
と書き換えられ、平均自由行程は、
λ = 1/(21/2nσ) (6)
となります。次に示すように、速度分布を考慮に入れても(6)式は変わりませんから、平均自由行程を求めるときにはこの(6)式(σは(2)式)が用いられます。
ここで、状態方程式 p= nkTを(6)式に代入すれば、
λ = kT/(21/2pσ) (7)
が得られ、平均自由行程λは圧力 p に逆比例することが判ります。
速度分布がマクスェル分布である場合
分子の速さは一定では無く、その速度分布がマクスウェル分布であると考えれば、かなり現実的な解が得られます。条件は以下のようになります。
・気体は1種類の分子から成っている。 ・気体分子は半径rの剛体球である。 ・気体分子の速度分布はマクスウェル分布である。
この場合、(1)式の v は分子の速さの平均値 v に、(5)式の21/2v はマクスウェル分布を持つ分子どうしの相対的な速さの平均値 u に置き換えなければなりません。 v は付録A-1で述べたように、(8kT/πm)1/2 です(kはボルツマン定数を、mは分子の質量を表す)。一方、u を数学的に求めることは少々面倒です。最も簡単なのは、速さの平均値の2乗と速さの2乗の平均値との違いを無視することで、ただちに u2 = 2v2 が得られます。実際には違いを無視することはできませんが、u に関する違いと v に関する違いがキャンセルして、結果としては u = 21/2v となります(注4)。従って、平均自由行程は、速さが一定と仮定して導いた(6)式と同じ形になります。
 具体的な例
具体的な例
常温(T=300K)における窒素ガスの平均自由行程を求めてみます。分子直径 d (=2r) を 3.7E-10 m(注5) とすれば、
λ = 0.68/p(Pa) cm (8)
となります。この式は、圧力を Pa 単位で代入すれば、平均自由行程が cm 単位で得られることを意味しています。例えば圧力が 1Pa のとき、平均自由行程は 0.7cm 程度です。真空の分野で慣用的に用いられる圧力単位 Torr を用いれば、
λ = 0.051/p(Torr) mm (9)
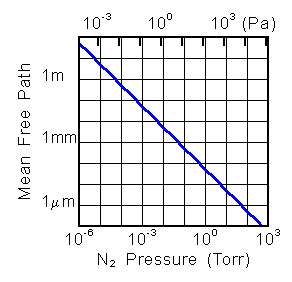
と表されます。右の図に示すように、大気圧(760Torr)では 0.1μm以下で、いわゆる高真空と呼ばれる 1E-6 Torr 程度の圧力では 50m にもなります。
2種類の分子から成る気体の場合
条件は以下のようになります。ただし3番目の条件については、気体分子の速さ va、vb が一定と考えても差し支えないことは上の説明と同じです。
・気体は2種類の分子a,bから成っている。 ・気体分子は半径ra,rbの剛体球である。 ・気体分子の速度分布はマクスウェル分布である。
気体分子 a に着目すると、(1)式は
λa = vaτ (10)
と書き換えることができます。分子が1種類の場合、(3)式より σvτn = 1 ですから、σvn は単位時間当たりの衝突(散乱)数、つまり衝突頻度を表していることが判ります。従って、相対的な速さを考慮した場合、2種類の場合の衝突頻度は {σana21/2va+σbnb(va2+vb2)1/2} であり、平均自由時間τは、
τ = 1/{σana21/2va+σbnb(va2+vb2)1/2} (11)
と表されます。分子の速さは熱平衡においては質量 m の平方根に逆比例することから、(10)式と(11)式をまとめますと、
λa = 1/{21/2σana+σbnb(1+ma/mb)1/2} (12)
が得られます。ここに、
σa = 4πra2 (13)
σb = π(ra + rb)2 (14)
であることは、(最も単純に考えた場合)の説明からわかると思います。
気体分子 b についても同様に導くことができますから、(12)式において、添え字 a と b を全て入れ替えればλb を表す式になります。
(注1)分子間にはファン・デル・ワールス力という引力が働くし、あまり分子どうしが接近すると強い斥力が働くことが知られている。 (注2)熱平衡であるから、衝突の度に向きは変わるが速さvは変わらないと考える。 (注3)散乱断面積の概念は、原子と原子だけで無く、原子核と原子核あるいは中性子と原子核など、粒子間の衝突を扱う場合に広く用いられている。ただし、(2)式が適用できるとは限らない。 (注4)速度の分布(速さの分布でないことに注意)は平均が0で分散がkT/mの正規分布であるから、相対速度の分布は、平均が0で分散が2kT/mの正規分布になるであろうと推測してもよいかもしれない。あるいは、誤差伝搬の法則から類推して理解するのもよいであろう。 (注5)E-10は10の -10乗であることを表す。
Rev.2 の修正個所: √ がかかる範囲が不明瞭なので、表記を 1/2 に改めた。
以上
このページは、高木郁二が担当している京都大学工学部物理工学科の講義・実験を補う資料として作成したものです。ご意見・お問い合わせはこちらまでお願いします。