 単純化して考えた場合
単純化して考えた場合「エネルギー理工学設計演習・実験2」別冊
1998.11.09
keywords: collision of gas molecules with wall
概要
気体分子の入射頻度(「壁を叩く気体分子の数」と表記されることも多い)が、分子の密度と平均速さに比例することを導きます。入射頻度は、気体における輸送現象を考える際に必要ですし、もちろん真空工学においても重要な値です。
 単純化して考えた場合
単純化して考えた場合
単位時間当たりに単位面積の壁に気体分子が衝突する数 F を、気体分子の入射頻度と呼ぶことにします。
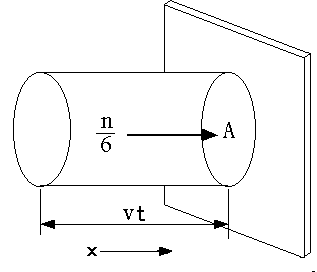
右図のように、断面積が A で、壁に垂直な円筒を考えます。気体分子の速さ v は一定であり、その運動方向は壁に垂直であるとすると、時間 t (注1)の間に壁に衝突(入射)し得る分子は、右図の円筒内に存在するものに限られます。実際には分子はあらゆる方向に運動していますが、単純に考えて、全分子の 1/6 (空間の3方向にそれぞれ正負の方向があるから) だけが壁の方向に向かっているものとします。円筒の体積は Avt ですから、時間 t の間に面積 A に衝突する分子数 N は、Avtn/6 で、従って Fは、
F = N/At = nv/6 (1)
と表されます。
一般式
実際の気体は速度分布を持っていることを考慮します。上の図において、v を x 方向の速度成分 vx に置き換えると、速度成分が vx(> 0)で、 壁から vxt 以内の距離にいる分子は、時間 t の間に壁に衝突します。最初は円筒内に存在していても、円で囲んだ部分の壁に衝突するとは限りませんが、円筒外に存在していた分子も、速度成分によっては円で囲んだ部分に衝突することもありますから、結局は Avxt の空間に存在していた分子が、そのまま円で囲んだ部分に衝突すると考えても構いません。 x 方向の速度分布を g(vx) としますと、g(vx)nAvxt 個の分子が時間 t の間に面積 A に衝突しますから、vx が 0 から ∞ までの全ての場合について足し合わせれば(積分すれば) N が得られます。
N = ∫g(vx)nAvxt dvx (2)
速度分布が、Maxwell の分布則に従うものとしますと、
N = Ant(m/2πkT)1/2∫vxexp(−mvx2/2kT)dvx (3)
と(2)式は書き直され、積分を実行すると、
N = Ant(kT/2πm)1/2 (4)
となります。ここで、気体分子の平均速さ v が (8kT/πm)1/2 であることから、入射頻度 F の一般式として、
F = N/At = nv/4 (5)
が得られます。理想気体の場合は n = p/kT ですから、(5)式は次のように表すこともできます。
F = p/(2πmkT)1/2 (6)
 上記の導出が納得できない人に
上記の導出が納得できない人に
面に垂直な円柱のみを対象として(5)式を導きましたが、考え方としては、半無限空間から面積Aに衝突する全ての分子を足し合わせる方が判りやすいかもしれません。
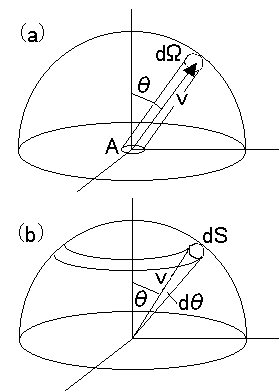
右図(a)のように、速さ v の半球を考えます。面 A から分子が出ていく向きに描いていますが、方向を全く逆にすれば衝突する方向になりますから、結局は同じことです。立体角 dΩ の方向に、速さ v で進む分子の割合は、速さの分布を f(v) としますと、f(v)dv(dΩ/4π) と表されます(注2)。また、(a)図に示した円柱の体積は Avcosθ ですから、この円柱内に存在し、速さが v である分子が衝突する数 dN は、時間 t を考慮しますと、
dN = nAtvf(v)cosθdv dΩ/4π (7)
と表されます。
(b)図に示すように、dΩ に相当する球面上の微小な面積を dS としますと、立体角の定義より、dΩ=dS/v2 となります。方向角の依存性はありませんから、θ〜θ+dθ で囲まれる球面上の帯の面積を dS と置きかえますと、dS = 2πvsinθ×vdθ と表され、dΩ = 2πsinθdθ となります(注3)。従って、N は
N = (nAt/2)∫vf(v)dv∫sinθcosθdθ (8)
と書くことができます。 dv についての積分範囲は 0〜∞ ですから、∫vf(v)dv は平均速さ v の定義そのものです。また、dθ についての積分範囲は 0〜π/2 ですから∫sinθcosθdθ = 1/2 です。以上より、
F = N/At = nv/4 (9)
を得ます。これは、(当然のことですが)(5)式と同じです。
実用的な式
圧力pの単位を Pa で表し、気体の分子量をMとすると、(6)式は、
F = 2.6E24 p/(MT)1/2 [1/m2s] (10)
と書き直すことができます(注4)。
常温常圧の窒素ガス(空気と考えてよい)の場合、F = 3E27 分子/m2s にもなりますが、 0.1mPa (〜1E-6 Torr) の高真空では、F = 3E18 分子/m2s です。固体表面の原子密度は 1E19 原子/m2 程度ですから、もし固体表面に入射した全ての分子が表面に吸着すると仮定しますと、表面は3秒程度で分子に覆われてしまうことになります(注5)。真空中で劈開、加熱、イオン衝撃等によって折角清浄な表面を作成しても、0.1mPa 程度の圧力では数秒の内に分子(=不純物)に覆われてしまうことになる訳です。この理由から、清浄な表面を観察するためには、10nPa (〜1E-10 Torr) 以下の超高真空が必要とされます。例えば 1nPa の場合、3000秒経過しても分子が覆う割合は1% 程度で、様々な測定をすることが可能になります。
(注1)分子どうしの衝突が起こらないような微小な時間である。 (注2)立体角とは半径が1の球の表面上に占める面積と定義され、単位は rad である。球全体の表面積は4πであるから、全立体角は 4π[rad] となる。 (注3)dΩについての積分範囲は半球全体であるが、この段階では方向角を積分したことになっており、dθについてのみ積分を実行すればよい。 (注4)E24 とは、10の24乗であることを表す。 (注5)既に吸着した分子の上に入射した分子は跳ね返ってしまうかもしれないから、この値は概算である。なお、清浄な表面に入射した分子が高い確率で表面に吸着され得ることは、多くの実験で確認されている。
以上
このページは、高木郁二が担当している京都大学工学部物理工学科の講義・実験を補う資料として作成したものです。ご意見・お問い合わせはこちらまでお願いします。