粘性とは？「エネルギー理工学設計演習・実験２」別冊
1999.03.12
keywords: coefficient of viscosity, viscous flow
概要
圧力が高い（平均自由行程λが代表長さ Ｌ よりも充分小さい）場合の、気体の粘性について説明し、粘性率が圧力に無関係であることを示します。逆の場合（λ≫ Ｌ ）については、その性質を利用したり、考慮することが少ないため、省略します。
粘性とは？
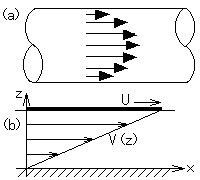
パイプに水を流すと、流れの速さは右図（ａ）のように、中心で最も早く、周辺で遅くなることは、よく知られています。これは水に粘り気、つまり粘性があり、動かないパイプの内壁に引きずられるように水が流れるためです。特殊な例を除いては、流体（気体や液体）は粘性を持っています。
粘性の程度を表す物性を粘性係数（粘度、粘性率）と言い、流体や温度によって異なります。常温常圧におけるいくつかの流体の粘性係数を cP という単位（後述します）で表すと、水：1.0、濃硫酸：27、グリセリン：1500、空気：0.018 です。言葉から直感的に判るように、粘い流体ほど粘性係数が大きくなっています。
水の上に板が浮かんでいるような状態（右上図（ｂ））を考えます。この板を ｘ 方向に速さ Ｕ でゆっくり動かしますと、粘性によって板の下にある水も同じ方向に動きますが、板から遠ざかるにつれてその速さＶは小さくなり、水の底では０になります。つまり、水の流れの速さ Ｖ は位置 ｚ の関数 Ｖ(z) になります。板を動かすためには力（流動応力）が必要で、粘性係数ηとは、その力が速度勾配に比例すると仮定したときの比例定数です。式で表すと、次のようになります。
f = −η(∂Ｖ/∂ｚ) (1)
簡単な導き方
平均自由行程λが代表長さ Ｌ よりも充分小さい場合の、気体の粘性係数を導いてみます。気体が管の中を流れている場合、代表長さは管の内径になります。
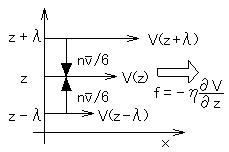
右図のように、ｘ方向に沿って気体が流れている状態を考えます。流れの速さは ｘ と垂直な位置 ｚ の関数であり、Ｖ(z) と表されるものとします。分子個々はランダムに熱運動しており、速さの平均値は ｖ ですが、均してみると ｚ の位置に応じて Ｖ(z) という速さを余分に持っていると考えればよいでしょう。
右図では、ｚ が大きいほど Ｖ も大きいように描いています。ある位置 ｚ を基準面として考えると、位置 ｚ-λ から来て z で他の分子と衝突して速さが Ｖ(z) となった分子は、運動量を ｍ[Ｖ(z) - V(z-λ)] だけ奪い、位置 ｚ+λ から来て ｚ で他の分子と衝突して速さが Ｖ(z) となった分子は、運動量を ｍ[Ｖ(z+λ) - Ｖ(z)] だけ失うことになります。ここにλは気体分子の平均自由行程で、簡単に考えるために、分子は ｚ 方向に速さ ｖ で運動していると仮定しました（注１）。このような仮定の下では、分子が運動する方向は xyz のいずれかであり、それぞれに正負の別があるので、分子の入射頻度は ｎｖ/6 と表されます（ｎ は分子の密度）。従って、位置 ｚ において単位面積単位時間当たりにもたらされる運動量の変化は、-(ｎｖ/6)ｍ[Ｖ(z) - V(z-λ)] - (ｎｖ/6)ｍ[Ｖ(z+λ) - Ｖ(z)] = -(ｎｖ/6)ｍ[Ｖ(z+λ) - V(z-λ)] となります。
ここで、「力」は運動量の時間的変化であることを考えると、「単位面積単位時間当たりにもたらされる運動量の変化」とは「単位面積当たりの力 = 応力」であることが判ります。従って、
ｆ = -(ｎｖ/6)ｍ[Ｖ(z+λ) - V(z-λ)] (2)
と表されます。（２）式の [ ] 内を一次の項まで展開すると（注２） Ｖ(z+λ) - V(z-λ) = Ｖ(z) + λ(∂Ｖ/∂ｚ) - Ｖ(z) + λ(∂Ｖ/∂ｚ) = 2λ(∂Ｖ/∂ｚ) となることと、ｍｎ = ρ (気体の密度) であることから、
ｆ = - (ρｖλ/3)(∂Ｖ/∂ｚ) (3)
を得ます。（３）式と（１）式を比較することにより、粘性係数 η は、
η = ρｖλ/3 (4)
となります。
（４）式を導く際に、分子の運動方向を６方向に限定しましたが、実際にはあらゆる方向にランダムに運動している筈です。このことを考慮すると、位置 ｚ で衝突する分子は平均して ｚ±2λ/3 の位置から飛来することになります[6]。つまり、上で述べたλは全て 2λ/3 で置き換えなければなりません。しかし、ランダムに運動している分子の入射頻度は ｎｖ/4 なので、結局はこれらが相殺して（４）式が導かれます。
粘性係数の単位は、（４）式からわかるように g/cm.s （ｃｇｓ単位系）で、poise （ポアズ）ともいいます。poise は単に P と書かれることもあり、cP とは centi-poise = 1/100 poise です。また、ｆ の単位が応力（圧力）であることと（１）式から、Pa.s （ＳＩ単位系) であることも容易に判ります。1 poise = 0.1 Pa.s です。
粘性係数ηの性質
分子の衝突に関する全散乱断面積をσとしますと、平均自由行程λは 1/√2ｎσ と表されますので、（４）式は、
η = ｍｖ/3√2σ (5)
となります。つまり、粘性係数は圧力に依存しません。圧力が減少すると、衝突する頻度（運動量の授受を行う機会）は減少しますが、次の衝突までの距離（運動量を伝える長さ）は増加し、これらの効果が相殺するためです。
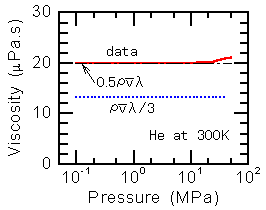実際、ヘリウムの熱伝導率（注３）は、右図に実線（赤）で示すように、0.1
MPa (大気圧) から 10 MPa（100気圧) までは圧力にほとんど依存していません。図中の破線（青）は、（５）式から求めた値です。ただし、σ
= πｄ2 ( ｄ = 0.218nm[6]） としました。
（４）式は単純化して導びかれた式であり、より現実的な式としては、
η = 0.5ρｖλ (6)
がよく用いられます[6]。この式は分子が堅い弾性球と見なせる場合に適用され、水素やヘリウム等が該当します。（６）式から求めた値を右図に重ねて示すと一点鎖線（黒）のようになります。実際の値に極めて近くなっていますが、これは、粘性係数から逆に（６）式によってλを求め、更にλからｄの値を求めているためです。つまり、分子直径ｄは一般に粘性係数から推算されており、このｄを用いて粘性係数を求めることは堂々巡りになってしまうのです。従って、右上の図は、粘性係数は圧力に依存しないことを示しているだけだと思って下さい。
次に温度への依存性を考えてみます。全散乱断面積σは、分子が剛体球であると仮定すると、分子直径 ｄ の２乗に比例するだけなので温度に無関係です。一方、平均速さ ｖ は、絶対温度 Ｔ の平方根に比例しますから、（５）式より粘性係数ηは温度の平方根に比例することが判ります。
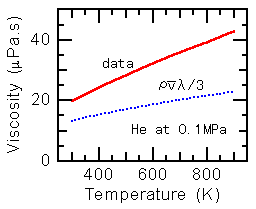上の例と同様に、0.1MPaでのヘリウムの粘性係数と（５）式による計算値とを比較しますと、右図のようになります。300Kにおける絶対値が異なっているのは（６）式を用いていないためですが、実際の値の温度依存性は、Ｔ0.5ではなく、Ｔ0.7程度になっています。これは、剛体球を仮定して分子直径
ｄを定数としたためと考えられます。例えばLennard-Jones
のポテンシャルを仮定すれば、温度が高いと分子どうしはより近くまで接近することができ、分子直径 ｄ は小さくなることになりますので、定性的には実際の値の傾向を説明することができます。
(注1) つまり、ｚ方向速度が ｖ で、ｘ方向速度が Ｖ(z) であると仮定している。通常、ｖ >> Ｖ であるから、平均自由行程λは定数と考えても差し支えない。 (注２) 図からはλは微小な距離に見えないかもしれないが、ｘ方向に流れが生じている領域の大きさはλよりもずっと大きい場合を考えている。 （注３） 日本機械学会編「伝熱工学資料（第４版）」丸善(1986)337.
以上
このページは、高木郁二が担当している京都大学工学部物理工学科の講義・実験を補う資料として作成したものです。ご意見・お問い合わせはこちらまでお願いします。