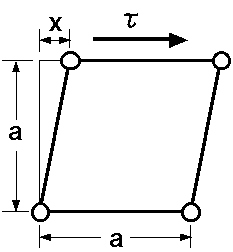
 (3)式におけるばね定数αを推定するために、一辺がaの単純立方格子結晶を考える。この結晶に応力τを加えたとき、右図のように、原子間距離当たりxだけ歪んだとすると、応力−歪の関係よりτ=Gx/a
(Gは剛性率) である。対象となる面積は1原子当たりa2 であるから、原子に働く力 F は、F= τa2
= Gax となる。この式とフックの式 F = αx とを比較すると、ばね定数αは Ga となる。従って(3)式より、
(3)式におけるばね定数αを推定するために、一辺がaの単純立方格子結晶を考える。この結晶に応力τを加えたとき、右図のように、原子間距離当たりxだけ歪んだとすると、応力−歪の関係よりτ=Gx/a
(Gは剛性率) である。対象となる面積は1原子当たりa2 であるから、原子に働く力 F は、F= τa2
= Gax となる。この式とフックの式 F = αx とを比較すると、ばね定数αは Ga となる。従って(3)式より、格子比熱と電子比熱への古典近似適用の妥当性について
2000.2.5 rev. 1998.7.25 I.Takagi
(概要)
常温付近の固体の格子比熱(原子熱)は Dulong-Petit の法則によってよく説明されるが、いくつかの固体については 3R という値からずれてしまう。また、金属中における自由電子による比熱への寄与は古典的な考え方では説明できない。古典的な考え方(古典近似)がどこまで適用できるのかを、不確定性原理を用いて検討する。
(不確定性原理)
「量子力学においては位置座標と運動量など互いに正準共役の関係にある2つの量がともに確定している状態がありえないことを述べる原理.」[1] で、不等式
ΔxΔp≧h/4π (1)
で表される(注1)。hはプランク定数である。一方、ある粒子の運動を古典的に扱うということは、代表長さLの中に存在している粒子の運動量pを記述できることを意味する。従って、もし Lとpが充分大きく
Lp≫h/4π (2)
であれば、不確定性原理による制限は無視でき、古典近似が成り立つはずである。h/pはド・ブロイ波長λを表すから、古典近似が成り立つ条件は L≫λ/4π と書き換えることもできる。
例として圧力Pが1気圧、温度Tが300 K の窒素ガス(乾燥空気とほぼ同じ)を考える。ガス分子の質量をm、ボルツマン定数をkとすると、ガス分子の運動量 p は (2mkT)1/2 である。m=4.6E-26 kg(注2)、k=1.38E-23 J/K、h=6.63E-34 Js より、λ=3.4E-11 m (0.034 nm) を得る。次に、容積 V の中に n 個のガス分子がある場合、理想気体を仮定すれば PV=nkT が成り立つ。分子1個当たりが占める空間が一辺 L の立方体であるとすると、nL3 =Vであるから、この2つの式より L=3.4E-9 m (3.4 nm) を得る。従って、代表長さ L は分子のド・ブロイ波長λよりも充分長く、古典近似が成り立つはずである。 L が大きいということは気体分子の密度が小さいことを意味するので、「希薄である」と表現することがある。
(金属中の自由電子)
電子間の相互作用を無視すると、自由電子は理想気体と考えることができるから、上の例と同様にして、ド・ブロイ波長が求められる。m=9.1E-31 kg より、λ=7.6 nm である。気体分子の場合と異なるのは、電子の質量が極めて小さいこと(最も軽い水素分子の約3700分の1)であり、そのためド・ブロイ波長が長い。一方、1個の金属原子当たりに1個の自由電子が存在するから、代表長さは金属原子の原子間距離程度と考えられる。つまり L〜0.2 nm であり、ド・ブロイ波長より小さいため、古典近似は成り立たない。自由電子に分配されるエネルギーは、古典統計力学で期待される値(3kT/2) よりもずっと小さくなってしまう(注3)。これが、自由電子による比熱の寄与(電子比熱)が常温においては少なく、格子比熱に較べて無視できる理由である。
(格子比熱について)
Dulong-Petitの法則は、原子を調和振動子として考え、等分配則を適用することによって格子比熱を説明している。1次元の調和振動子のエネルギーは、p2/2m + αx2/2 である。ただし、αはばね定数、xは変位量である。等分配則によればそれぞれの項の平均エネルギーは kT/2であるから、運動量の目安は p=(mkT)1/2、代表長さの目安は L=(kT/α)1/2 となる(後者ではxの平均値をLとおいた)。従って、古典近似が成り立つ条件は、Lp=kT(m/α)1/2 =kT/ω≫ h/4π である。ここにωは調和振動子の角振動数で、
ω = (α/m)1/2 (3)
で与えられる。いま、
Θ≡hω/4πk (4)
とおけば、古典近似の条件は T≫ Θ と書き換えられる。Θは温度の次元を持っており、特性温度(注4)と考えることができる。つまり特性温度Θが、対象としている温度(この場合は常温)に較べて充分低ければ、Dulong-Petitの法則が成り立つ筈である。
 (3)式におけるばね定数αを推定するために、一辺がaの単純立方格子結晶を考える。この結晶に応力τを加えたとき、右図のように、原子間距離当たりxだけ歪んだとすると、応力−歪の関係よりτ=Gx/a
(Gは剛性率) である。対象となる面積は1原子当たりa2 であるから、原子に働く力 F は、F= τa2
= Gax となる。この式とフックの式 F = αx とを比較すると、ばね定数αは Ga となる。従って(3)式より、
(3)式におけるばね定数αを推定するために、一辺がaの単純立方格子結晶を考える。この結晶に応力τを加えたとき、右図のように、原子間距離当たりxだけ歪んだとすると、応力−歪の関係よりτ=Gx/a
(Gは剛性率) である。対象となる面積は1原子当たりa2 であるから、原子に働く力 F は、F= τa2
= Gax となる。この式とフックの式 F = αx とを比較すると、ばね定数αは Ga となる。従って(3)式より、
ω = (Ga/m)1/2 (5)
を得る。実際の結晶は単純立方格子では無いなど、(5)式は粗い見積りであることに注意せよ。 a を格子定数と仮定すれば、G の値より特性温度 Θ を求めることができる。
下の表は、いくつかの固体元素における特性温度 Θ (注5)と常温付近 (T〜 300 K) での定圧モル比熱の値である。銅では古典近似の条件 T≫Θ が成り立っており、モル比熱は 3R (= 24.9 J/K・mol) にかなり近い。珪素では T≫Θとは言い難く、やや 3R から外れている。ベリリウムでは T と Θ は同じ程度であり、モル比熱の値は明らかに 3R よりも小さい。Θ が元素によって異なるのは、主に m に依るものであることは表からわかるであろう。 a や G はそれほど元素に依存していないが(注6)、m の値は(当然の事だが)桁が異なっているからである。従って、C や B などの軽い元素についても古典近似が成り立たないと推測され、事実、3R という値よりもかなり小さくなっている(具体的には Dulong-Petitの法則の項を参照されたい)。
| 元素 | Cu | Si | Be |
| a (m) | 3.61E-10 | 5.43E-10 | 3.59E-10 |
| m (kg) | 1.05E-25 | 4.66E-26 | 1.50E-26 |
| G (Pa) | 4.83E+10 | 7.95E+10 | 1.43E+11 |
| ω (1/rad) | 1.29E+13 | 3.04E+13 | 5.85E+13 |
| Θ (K) | 49 | 116 | 224 |
| C (J/K・mol) | 24.1 | 21.4 | 16.0 |
(参考文献)
[1] 「理化学辞典」第4版 岩波書店(1987). より抜粋
以上
2000.2.5 追記1: このページは、不確定性原理から古典近似の成り立つ範囲を推測することを目的としており、成り立たない場合の電子比熱や格子比熱は説明していない。これらについては固体物理学の教科書を参照されたい(デバイの比熱式では、T=ΘD(デバイ温度)で Dulong-Petit の法則が成り立つことに注意せよ)。
2000.2.5 追記2:「フックの式」を「フィックの式」と記載していました。また、文章中の数値に誤りがありました。お詫びして訂正します。
このページは、高木郁二が担当している京都大学工学部物理工学科の講義・実験を補う資料として作成したものです。ご意見・お問い合わせはこちらまでお願いします。