「エネルギー理工学設計演習・実験２」別冊

Ａ−９-1　コンダクタンスの一般式と通過確率（クラウジング係数）

2001.12.13

keywords: conductance, Clausing's factor, molecular flow

概要

　Ａ−９の付録です。分子流領域におけるコンダクタンスの一般式を導き、その式中で重要な通過確率（クラウジング係数）について説明し、Ａ−９中の補正係数 Ｋ について考察します。

コンダクタンスの一般式

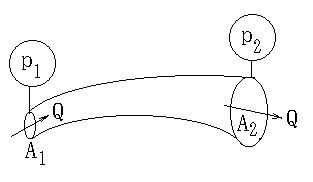
　Ａ−９で説明したオリフィスでは、厚さが無限に小さいために、一方からオリフィスに入射した気体分子は、必ず他方に通過します。逆方向についても同じです。これに対し、右図のような導管では、有限の長さがあるために、一方から入射した分子は何度も管壁に衝突して跳ね返り、入射した側から、あるいは他方の側から出ていくことになります。

　右図のように、一方の入口１の開口面積が Ａ₁、他方の入口２（注１）の面積が Ａ₂ の導管を考え、正味の流量を Ｑ、それぞれの開口部における圧力を ｐ₁、 ｐ₂ とします。入口１から入った分子が入口２から出ていく確率を P₁₂、入口２から入った分子が入口１から出ていく確率を P₂₁ と表すことにすると、オリフィスと同じように考えることができます。つまり、入口１から入って入口２に出ていく分子の数は、面積 Ａ ₁に対する入射頻度に確率 P₁₂ を乗じた値になるので、Ａ₁ｎ₁P₁₂ｖ/４ と表されます。ここで ｎ₁ は圧力 ｐ₁ における分子の密度です。分子の数を入射頻度を ｎ₁ で割れば体積流量となり、更に圧力 ｐ₁ を乗じれば質量流量（体積の流れ×圧力） になりますから、この値をＱ₁ と書くと、

　Ｑ₁ = Ａ₁ｐ₁P₁₂ｖ/４　　(1)

と表されます。同様に、入口２から入って入口１に出ていく流量 Ｑ₂ は Ａ₂ｐ₂P₂₁ｖ/４ なので、正味の流量 Ｑ (= Ｑ₁ - Ｑ₂) は、

　Q = （Ａ₁ｐ₁P₁₂ - Ａ₂ｐ₂P₂₁）ｖ/４ 　　(2)

となります。ここで、p₁ = p₂、つまり圧力差が無い状態を考えますと、正味の流量 Q は 0 になる筈ですから、(2)式より、

　Ａ₁P₁₂ = Ａ₂P₂₁　　　(3)

という関係が得られますので、(2)式は、

Q = Ａ₁P₁₂（ｐ₁ - ｐ₂）ｖ/４　　　(4)

となります。コンダクタンス Ｃ と流量 Ｑ との関係式　Ｑ = Ｃ(ｐ₁ - ｐ₂) と (4)式を比較することにより、

　Ｃ = C₁P₁₂　　(5)

が得られます。ただし、

　Ｃ₁ ≡ Ａ₁ｖ/４　　　(6)

です。

通過確率（クラウジング係数） W

　(5)式および(6)式がコンダクタンスの一般式です。これらの式を少し眺めてみることにします。開口面積が Ａ のオリフィスでは、Ａ₁ = Ａ であり、管壁との衝突が無いことから、P₁₂ = 1 です。このとき、Ｃ = Ｃ₁ = Ａｖ/４ となり、当然のことですが、Ａ−９で導いた(3)式に等しくなります。つまり、コンダクタンスの一般式とは、入口と同じ面積を持つオリフィスに、Ｐ₁₂ という確率を乗じた形をしていることがわかります。この確率を通過確率と呼びます。あるいは、クラウジング係数（Clausing's factor）を呼ぶこともあります。以下では、通過確率 P₁₂ を Ｗ と表記することにします。

　通過確率をわざわざ用いることを不思議に思うかもしれません。例えば右図（ａ）に示すように、断面が円形の直管内を分子が管壁に衝突して跳ね返る（反射する）場合に、剛体球が質量無限大の相手に弾性衝突すると考えると、　軸方向の運動量は保存されたまま、分子は入射角と等しい反射角で反射して進行していくでしょう。このときの通過確率は１になる筈です。しかし実際には、（ｂ）に示すように、分子はランダムに跳ね返ると考えなければ、コンダクタンスの実測値を説明することはできません。

　壁を微視的に見れば、大小さまざまな凹凸面になっているでしょう。この面に分子が入射すると、ある位置と少し離れた他の位置で跳ね返ったときの方向は全く異なることがあり得ます。その結果、巨視的に見れば、分子はどの方向にも等しい確率で跳ね返ると考えられています。あるいは、分子は極く短い時間ながらも表面に滞留した後に、入射してきた方向の記憶を失ってから任意の方向に出ていくこともあるかもしれません。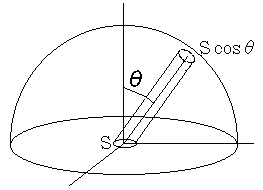

　このようなランダムな跳ね返りを、余弦法則と表現することがあります。右図に示すように、微小な面積 Ｓ の領域で跳ね返った分子が、法線から角度θの方向に進む数は、法線方向に進む数の cosθ倍になることが、名前の由来です。微小な面積 Ｓ の球面への投影面積が Ｓcosθ となるからです。

　一般に、通過確率 Ｗ を理論的に求めることは容易ではありませんが、断面が円形で長い直管については、跳ね返りが余弦法則に従うと仮定すれば解析的に求めることができます[1]。

　W = ８ａ／３Ｌ　　(7)

ここに、ａ と Ｌ は、それぞれ管の半径と長さです。興味のある方は、参考図書[1]のpp.32-33 を参照下さい。Ａ−８ (9)式はこのようにして導かれた式です。

矩形管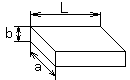

　右図のような、断面が矩形（辺の長さは ａ と ｂ）で、長さが Ｌ の管（ａ≪Ｌ および ｂ≪Ｌ） の場合、Ａ−９では Ｋ という補正係数を用いてコンダクタンスを求めましたが、参考図書[3] p594 (11.60)式及び(11.61)式に通過確率Ｗが示されています（注２）。興味のある方は参照下さい。ここに与えられたＷを用いると、Ａ−９ (14)式中のＫは、

　Ｋ = ３(１＋ａ／ｂ）Ｙ／８　　(8)

と表されます。ここに Ｙ は ａ／ｂ の関数であり、(11.61)式で与えられています。Ｙを(8)式に代入して得られた Ｋ の値を、ａ／ｂ の関数として図に示します。横軸が対数目盛であることに注意してください。Ａ−９では、ｂ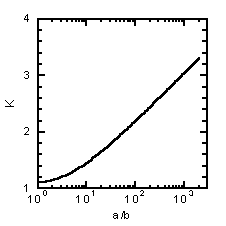／ａ に対する Ｋ のいくつかの値を示していますが、右図はａ／ｂという逆数の形にして、値の範囲を拡げて図示したものです。ａ／ｂの変化に対して、Ｋ の変化はゆるやかであることがわかります。例えば、ａ／ｂ = 1000 という大きい数値に対しても、Ｋ は ３ 程度にしかなりません。

Ｗ と Ｋ について

　Ａ−９(10)式を再掲します。

　Ｃ = ４ＫＡ²ｖ/３ＢＬ　　(A-9-10)

この式を(6)式を用いて書き換えると、

　Ｃ = Ｃ₁×１６ＡＫ／３ＢＬ　　　(9)

となります。(9)式と(5)式を比較すると、通過確率（Ｗ = P₁₂） は

　Ｗ = １６ＡＫ／３ＢＬ 　　　(10)

と表されます。この式は、コンダクタンスは、衝突する壁の総面積 ＢＬ （衝突する数）に逆比例し、分子が自由に運動できる空間の断面積 Ａ に比例することを表しており、直感的に分かりやすい形になっています。同じ断面積で、周長が最も短い図形は円ですから、(10)式は円の場合に Ｋ ＝ １ となるように係数を決めているようです。従って、Ｋ が １より小さくなることはありません。また、上の矩形管の例で示したように、ａ／ｂ が非常に大きいような場合でも、Ｋ は１より大きく外れることもありません。このようなことから、任意の断面を持つ管（ただし、断面の形状は一様で、周長Ｂは管の長さＬよりも充分小さい）の場合、２倍程度の違いを覚悟すれば、Ｋ = １ としても構わないでしょう。

　(10)式を用いて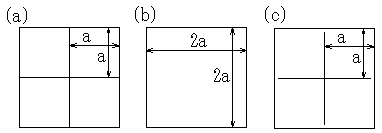少し遊んでみます。右図（ａ）と（ｂ）のように、断面積が同じ（４ａ²）で、長さ Ｌ も等しい管を考えます。コンダクタンスは、Ａ−９(10)式を用いて求めることができますが、ここでは、断面積が等しいことから、(10)式の通過確率 Ｗ を求めてみます。（ａ）の場合、一辺が ａ の正方形が４個集まっていますので、全周長は １６ａ です。一方、（ｂ）の周長は ８ａ です。(10)式中、他の数値は同じですから（注３）、（ｂ）の通過確率、つまりコンダクタンスは（ａ）の２倍になります。壁の面積分だけ（ａ）の方は分子が通過しにくくなっているわけです。断面積が同じでも、形状によって、コンダクタンスは異なった値になることがわかります。

　次に、(c)のように、一辺が ２ａ の正方形の管に、十字型の板を入れた状態を考えます。板と管壁との隙間が充分小さいと、分子が板や管の壁に衝突する総数は (a) の場合とほとんど変わらないので、コンダクタンスは （ａ） の値とほぼ同じであり、（ｂ） の値の約半分になることが予想されます。このように故意に板を入れるようなことはあまり無いでしょうが、コンダクタンスを考える上で参考になればと思います。

(注1) 　分子はどちらの開口部からも入射し、どちらの開口部からも出ていくことができるので、「入口」と表現した。正味の流れの方向を考え、「出口」と読み替えても構わない。　(注２) 　参考にした初版第１刷では、(11.61)に誤植があると思われる。等号が２個あり、右側の等号を＋に置き換えないと、同書 表11.4 の数字が得られないし、(11.62)式の Ｙ(δ) を導くこともできない。なお、(11.62)式の Ｙ(δ) は、(11.61)式の右辺各項において、1+δ² = (δ+1/2δ)²と近似し、第２項については、１次まで展開すると得られる。かなりの余談ではある。　（注３）　(a)における Ｋ の値は、正方形における Ｋ の値、つまり(b)の場合と同じだと考えてよい。腑に落ちなければ、一辺がａである矩形管のコンダクタンスをＡ−９(14)式から求め、４個が並列接続されているので、４倍すれば全体のコンダクタンスが得られる。これを Ｃ₁ で割っても Ｗ を求めることができるので、比較してみるとよい。

以上

このページは、高木郁二が担当している京都大学工学部物理工学科の講義・実験を補う資料として作成したものです。ご意見・お問い合わせはこちらまでお願いします。