1998.10.16 I.Takagi
(概要)
単体の代表的な結晶構造としては、ｈｃｐ、ｆｃｃ、ｂｃｃ がありますが、これらは金属性の結晶です。ダイアモンド型や黒鉛型、アンチモン型等も単体の結晶ですが、結合は非金属性です。ここでは講義の補足としてダイアモンド型について説明します。
(正四面体を重ねる)
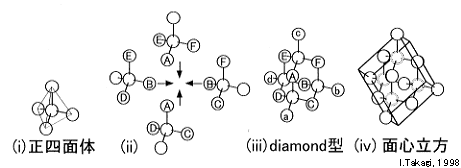
ダイアモンドは共有結合性の結晶で、１つの原子から結合の「手」が４本出ています。隣接する原子は４個で、下図（i）に示すように、これらの原子は正四面体を形成しています。従って、図（ii）に示すように、正四面体の角どうしを重ねていけば、つまり、原子Ａ〜Ｆをそれぞれ重ねていけば、図（iii）のようなダイアモンド構造になります。
ここで、原子Ａ〜Ｆに注目すると、これらは八面体を形成しています。更に、原子ａ〜ｄに注目すると、ａ-Ｃ-ｂ、ｂ-Ｆ-ｃ、ｃ-Ｅ-ｄ、ｄ-Ｄ-ａ、ｄ-Ｂ-ｂはそれぞれ、直線になっています。そこで、図（iii）でアルファベットを付けた原子のみに注目し、このような並び方をする結晶構造を考えてみると、図(iv）に示すように面心立方の一部であることが判ります。
(面心立方から考える)
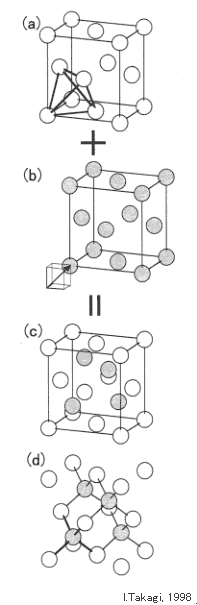
上記より、ダイアモンド型構造は面心立方を含んでいることが予想されますので、今度は面心立方構造から考えてみます。右図(a)に示すように、立方の角の原子と、隣接する面心位置の３個の原子は、四面体を形成してます。格子定数を ａ とすると、各辺の長さはどれも ａ/√2 ですので、これは正四面体です。
この正四面体の中心（注１）に図（ｂ）のようなもう一つの面心立方格子を重ねてみます。原子に区別はありませんが、格子が異なることを示すために、薄灰色で表しています。
重ね合わせた方の格子の中で、最初の格子の内側に配置される原子は、図（ｃ）に示すように４つだけで、当然のことながら、図（ｄ）に示すように、いずれも正四面体の中心に位置しています。
以上のことから、ダイアモンド型構造は、２つの面心立方格子が重なった複合格子であることが判ります。
(注1) 正四面体の中心は、面心立方体の対角を結んだ線上の、角から1/4の距離にある。正四面体の１辺がａ/√2 であることと、対角線の長さが ａ√3 であることから、容易に判るので、興味のある者は確かめてみよ。
以上
このページは、高木郁二が担当している京都大学工学部物理工学科の講義・実験を補う資料として作成したものです。ご意見・お問い合わせはこちらまでお願いします。