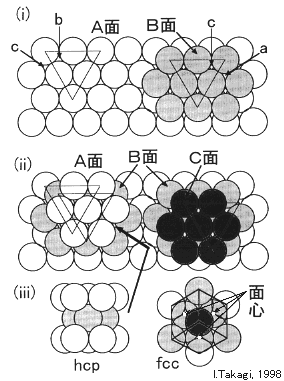
 同じ大きさの球を平面に密に並べると、右図(i)の白丸のようになります。これを、便宜上、A面と呼ぶことにします。A面上に球を積み重ねる場合、真上に並べたのでは最密にならず、b点またはc点の上に配置すると最も密になります。そこで、b点の上に球を並べることにし、できた面をB面と呼ぶことにします。
同じ大きさの球を平面に密に並べると、右図(i)の白丸のようになります。これを、便宜上、A面と呼ぶことにします。A面上に球を積み重ねる場合、真上に並べたのでは最密にならず、b点またはc点の上に配置すると最も密になります。そこで、b点の上に球を並べることにし、できた面をB面と呼ぶことにします。1998.10.15 I.Takagi
(概要)
結晶中の原子を同じ大きさの剛体球と考えると、最も密になるように積み重ねていく方法は何通りかあります。ここでは、最密充填構造である六方稠密構造(hcp)と面心立方構造(fcc)が、どのように積み重なっているかを説明します。
(面の重ね方)
 同じ大きさの球を平面に密に並べると、右図(i)の白丸のようになります。これを、便宜上、A面と呼ぶことにします。A面上に球を積み重ねる場合、真上に並べたのでは最密にならず、b点またはc点の上に配置すると最も密になります。そこで、b点の上に球を並べることにし、できた面をB面と呼ぶことにします。
同じ大きさの球を平面に密に並べると、右図(i)の白丸のようになります。これを、便宜上、A面と呼ぶことにします。A面上に球を積み重ねる場合、真上に並べたのでは最密にならず、b点またはc点の上に配置すると最も密になります。そこで、b点の上に球を並べることにし、できた面をB面と呼ぶことにします。
B面の上に最密に積み重ねるためには、a点の上かc点の上かに並べていくとよいでしょう。a点の上に並べた場合には、図(ii)の左側に示すように、A面と同じ配置になります。c点の上に並べた場合には、図(iii)の右側に示すように、AやBとは別の面になります。この面をC面と呼ぶことにします。
(hcpとfcc)
ABAと積み重なった面を、図(ii)に示した矢印の方向から、真横に見てみると、図(iii)の左側のように見えるでしょう。これが、六方稠密構造(hcp)で、それぞれの面(稠密な面)のミラー指数は (0001) です(注1)。
一方、ABCと積み重なった面を、図(ii)の真上から見ると、図(iii)の右側に示したような図形を取り出すことができます。これが面心立方構造(fcc)で、サイコロの1つの角を床に立てて、上から見たような形になっています。それぞれの面のミラー指数は (111) です。図では少し判りにくいかも知れませんが、B面(薄い灰色)の矢印で示した3つの球は、”面心”の部分(白抜きでその中心を示しています)で、残りの外側にある3つの球は”立方”の角の部分です。
(注1) 六方晶の場合には、六角形の辺の3方向+軸方向を座標にとった4軸で格子位置を表すことが多く、これに対応した4成分のミラー指数が用いられる。
以上
このページは、高木郁二が担当している京都大学工学部物理工学科の講義・実験を補う資料として作成したものです。ご意見・お問い合わせはこちらまでお願いします。